에라토스테네스의 체

‣ 에라토스테네스의 체(Eratosthenes' sieve)

고대 그리스의 수학자 에라토스테네스가 고안한 소수를 찾는 알고리즘

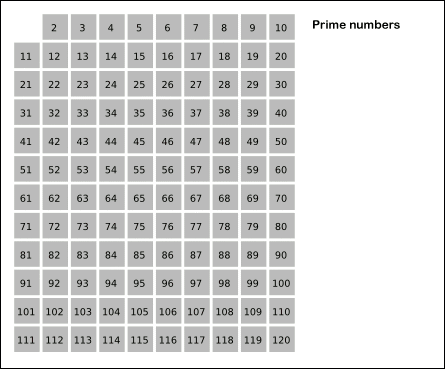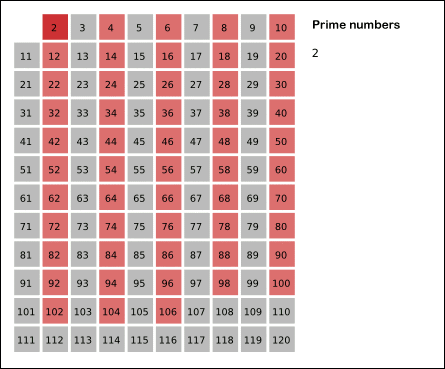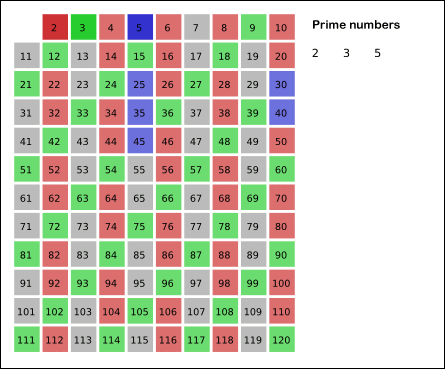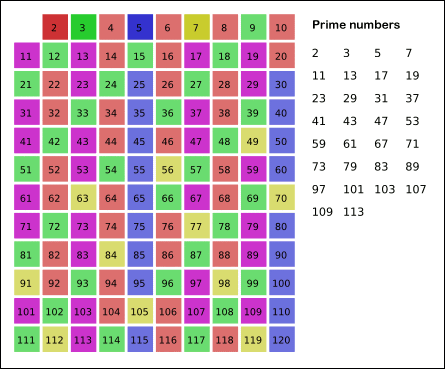
아래의 사진처럼 마치 체를 치듯이 수를 걸러내어 소수만 남기기 때문에, 에라토스테네스의 체 라고 부른다.

---

‣ 동작 방식

에라토스테네스의 체는 임의의 정수 n이 있으면 그 이하의 소수들을 $O(nloglogn)$의 시간 복잡도로 전부 찾아낼 수 있는 상당히 효율적인 알고리즘이다.

에라토스테네스의 체는 다음과 같은 원리로 진행된다.

1. 각 수에 대해 그 수의 배수를 모두 제거하는 작업을 수행한다.

2. 2의 배수를 제거할 때 $\frac{n}{2}$ 번, 3의 배수를 제거할 때 $\frac{n}{3}$ 번, 4의 배수를 제거할 때 $\frac{n}{4}$ 번 ...이런 식으로 진행된다.

3. 따라서 시간 복잡도는 $\frac{n}{2}+ \frac{n}{3}+ \frac{n}{4}+…+1=n( \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4}+…)$가 된다.

4. 여기서 $\frac{1}{2}+ \frac{1}{3}+ \frac{1}{4}+…$는 조화 급수로, 그 합이 $loglogn$에 근접하다는 것이 수학적으로 증명되어있다.

5. 그러므로 전체 시간 복잡도는 $O(nloglogn)$이 된다.

이런 시간 복잡도를 가지기에, 에라토스테네스의 체는 소수를 찾는 알고리즘 중에서 매우 효율적인 알고리즘으로 꼽힌다.

---

‣ 코드

[Python]

def prime(n):
	seive = [True]*n

	m = int(n**0.5)
	for i in range(2, m+1):
		if seive[i] == True:   
			for j in range(i+i, n, i):
				seive[j] = False

	return [i for i in range(2, n) if seive[i]==True]

간단한 코드 설명

• seive = [True]*n
  • 길이가 n인 boolean 리스트를 생성해서 전부 True로 초기화한다.
  • 최종적으로 남은 True의 인덱스는 모두 소수가 되고, False인 인덱스는 합성수이다.

• m = int(n**0.5)
  • n의 제곱근을 구하고, 그 값을 정수로 변환하여 m에 저장.
  • m 이하의 숫자만 확인해도 n 이하의 모든 숫자에 대한 소수 여부 판별이 가능하다.*

• for i in range(2, m+1):
  • 2부터 반복문을 돌리는데, 0과 1이** 소수가 아니기 때문이다.

• if seive[i] == True::
  • 현재 숫자 i가 소수인지 확인

• for j in range(i+i, n ,i):
  • 만약 위에서 검사한 i가 소수라면 진행된다.
  • seive 리스트 내에 존재하는 i의 배수는 1과 자신 이외에i를 약수로 가지기 때문에 전부 합성수다.
  • seive[j]=False를 해준다.

return [i for i in range(2, n) if seive[i]==True]:

• 2부터 n−1까지의 숫자 중 seive 리스트에서 True로 표시된 숫자만 선택하여 결과 리스트를 반환

• 이 결과 리스트는 n 이하의 모든 소수를 포함한다.

필자가 작성한 코드라 오류가 있을 수 있다.

더 효율적인 코드를 직접 작성하면서 외우는 것을 추천한다.

---

‣ 관련 백준 문제

본인이 풀어본 문제 중 괜찮았던 것을 추려서 추천한다.

• 2960번: 에라토스 테네스의 체
  • https://www.acmicpc.net/problem/2960

• 17103번: 골드바흐 파티션
  • https://www.acmicpc.net/problem/17103

• 1644번: 소수의 연속합
  • https://www.acmicpc.net/problem/1644

Uploaded by N2T