DFS와 BFS는 대표적인 그래프 탐색 알고리즘이다.
가장 머리 속에 남아있는 설명은 학부시절 들었던 설명인데,
"DFS는 내가 보려는 드라마 시리즈들을 쭉 정주행 하는 것이고, BFS는 한 회씩 두루두루 보는 것이다." 라는 것
기본 구현에 익숙해지면 응용하는 문제들을 해결하는 데에 도움이 되기 때문에, 백지에 바로 작성이 가능해 질 때까지 보는 중..
📎 백준 1260 문제를 바탕으로 글을 작성한다.
Depth-First Search(DFS)
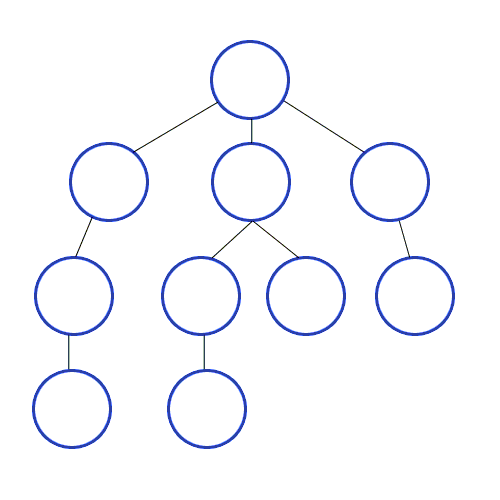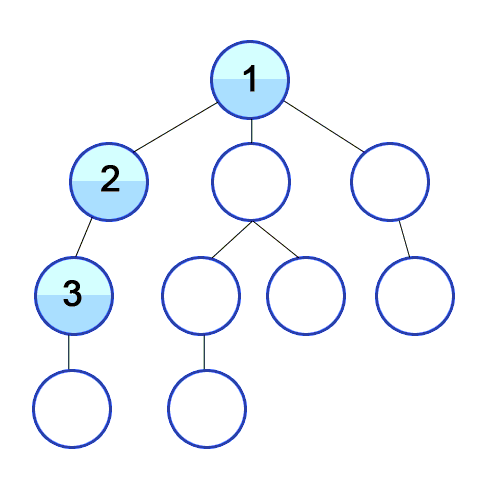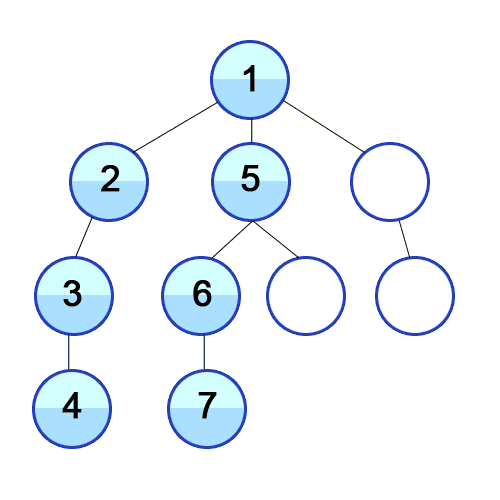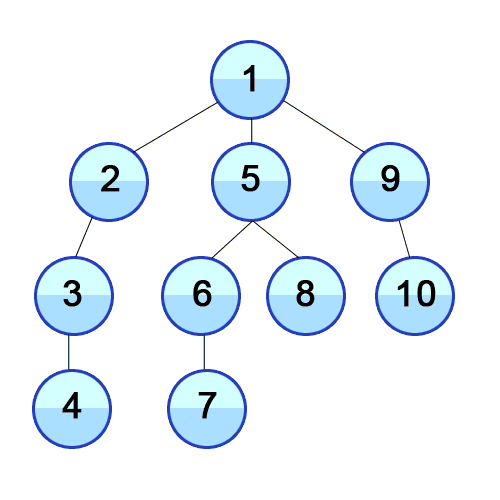
보통 Stack 혹은 재귀를 사용해 구현한다.
각 방법의 기본 구현 코드와 해당 방법을 사용했을 때의 장점을 살펴보겠다.
Stack을 사용한 구현
fun dfsWithStack(graph: ArrayList<ArrayList<Int>>, index: Int) {
val visited = MutableList(graph.size) { false }
val stack = arrayListOf<Int>()
stack.add(index)
while (stack.isNotEmpty()) {
val index = stack.removeAt(stack.lastIndex)
if (!visited[index]) {
visited[index] = true
print("$index ")
for (i in graph[index].size - 1 downTo 0) {
if (graph[index][i] == 1 && !visited[i]) {
stack.add(i)
}
}
}
}
}java.util Stack을 사용해도 좋지만, 순수 kotlin코드로 작성해 보고싶어 kotlin.collection의 ArrayList를 사용해서 작성했다.
데이터의 크기가 매우 크거나, 탐색 과정에서 유연한 컨트롤이 필요한 경우 Stack을 사용하는게 유리하다.
재귀를 사용한 구현
fun main(){
val graph = arrayListOf<ArrayList<Int>>(...)
val visited = MutableList(graph.size){ false }
dfs(graph, 0, visited)
}
fun dfs(graph: ArrayList<ArrayList<Int>>, index: Int, visited: MutableList<Boolean>) {
visited[index] = true
print("$index ")
for (i in 0 until graph[index].size) {
if (graph[index][i] == 1 && !visited[i]) {
dfs(graph, i, visited)
}
}
}재귀를 사용할때는 방문을 확인하는 visited 리스트를 인자로 넘겨줘야한다.
보통 데이터 크기가 1000~10000 정도의 작은 크기의 데이터를 다루는 경우에 적합하다.
데이터 크기가 십만 이상의 경우 Stack으로 구현하는 것을 고려해보는 것이 좋다.
Breadth-First Search(BFS)
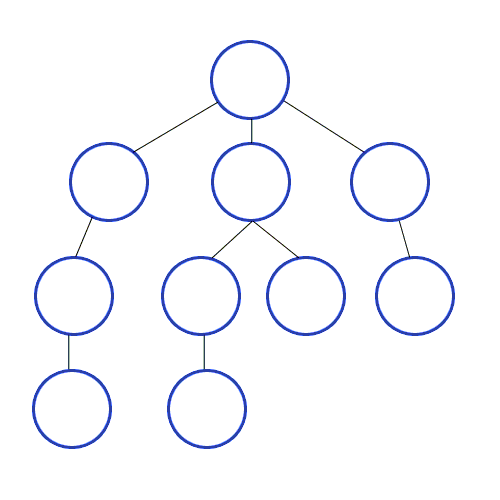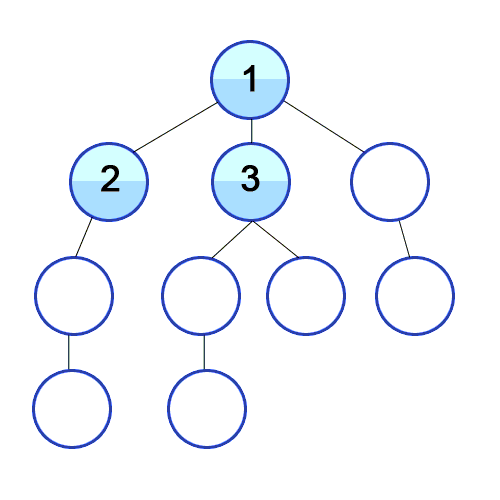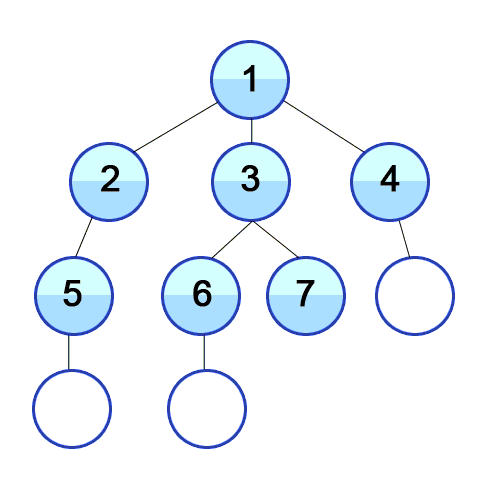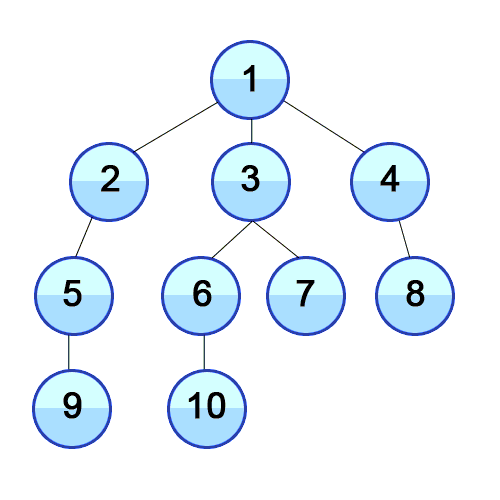
최단경로 탐색(Search)과 노드 레벨 순환(Level-order Traversal)에 사용한다.
큐(Queue)를 사용해서 구현하는데, 보통 Deque를 사용하는게 편하다.
fun bfs(graph: ArrayList<ArrayList<Int>>, index: Int) {
val queue = ArrayDeque<Int>()
val visited = MutableList(graph.size) { false }
queue.addLast(index)
visited[index] = true
while (queue.isNotEmpty()) {
val next = queue.removeFirst()
print("${next + 1} ")
for (i in 0 until graph[next].size) {
if (graph[next][i] == 1 && !visited[i]) {
queue.addLast(i)
visited[i] = true
}
}
}
}'CS > Algorithm' 카테고리의 다른 글
| 에라토스테네스의 체 (2) | 2023.10.20 |
|---|---|
| 유클리드 호제법(Euclidean algorithm) (2) | 2023.10.14 |
| N진법 (1) | 2023.10.04 |
| 힙(Heap) (0) | 2023.03.01 |
| 스택(Stack) (0) | 2023.02.27 |
